«Прямая» и «Плоскость» в плоской геометрии Евклида.©

В.И.Шендеров

Несколько тысячелетий математики пытаются, с одной стороны, доказать пятый постулат Евклида, а с другой стороны, удивляются, зачем он был добавлен Евклидом к первым четырем.

Пятый постулат всегда считался лишним.

Одна из его формулировок гласит, - «На плоскости через точку, находящуюся вне прямой, можно провести только одну прямую, параллельную данной».

Вспомним принятые Евклидом определения и свойства:

Из определения «Точка есть то, что не имеет частей» следует, что точка является отрезком прямой, длина которого равна его ширине. Следовательно, точка является частью прямой или частным случаем отображения прямой и, в то же время, длина ее и ширина не равны нулю, так как в этом случае точка не существовала бы;

Из определения «Прямая есть такая линия, которая одинаково расположена ко всем точкам» из предыдущего определения следует, что прямая линия – это плоскость, ширина которой равна ширине точки.

Следовательно,  прямая линия - часть плоскости или частный случай отображения плоскости;

Из определения «Плоскость есть поверхность, которая одинаково расположена ко всем прямым на ней лежащим» следует, что плоскость может состоять из точек, прямых линий или других плоскостей совпадающих с данной.

Отсюда следует, что плоскость это основное понятие, а точка и прямая есть частный случай плоскости.

Продолжая рассуждать в том же духе, получаем крамольную мысль, если основное понятие состоит из частных случаев, то и само понятие должно представлять частный случай.

В планиметрии Лобачевского-Бойяи через точку вне прямой на плоскости можно провести сколько угодно различных прямых, параллельных данной. Это – аксиома.

В планиметрии Римана через точку вне прямой нельзя провести ни одной прямой, параллельной данной. И это утверждение тоже аксиоматизируется. Казалось бы, что крамольного может быть в этих аксиомах? Где может быть неточность, которая столько лет ставит в тупик многих ученых? Неточность кроется в одном определении и это определение - понятие «ПЛОСКОСТЬ».

Постулируя это определение, как АБСОЛЮТНАЯ ПЛОСКОСТЬ, мы попадаем в нереальный двумерный мир барона Мюнхгаузена.

            В реальном трехмерном мире – Плоскость есть поверхность с радиусом кривизны, стремящимся к бесконечности.

Отсюда получаем, что Прямая есть такая линия, которая одинаково расположена ко всем точкам поверхности, с данным радиусом кривизны.

Радиус кривизны плоскости, а с ней и линии может быть любым и определяется он конкретными силами, действующими на плоскость в рассматриваемой кривой области, а не в прямоугольной.

Отсюда и реальная точка, имеющая длину, ширину и толщину так же является кривой поверхностью. Для опровержения этого попробуйте найти прямой участок на поверхности круга или шара. 

            Вероятно, это и есть то,  что ставил под сомнение в своей геометрии Евклид, вводя в геометрию пятый постулат. Пятый постулат придает плоскости Евклида свойства АБСОЛЮТНО ПЛОСКОЙ поверхности. Введение понятия кривизны, выводит геометрию Евклида из нереального плоского двумерного мира в реальный кривой трехмерный мир.

Двумерная абсолютно плоская геометрия Евклида становится частным случаем при условии, что радиус кривизны рассматриваемой плоскости или кривой стремиться к бесконечности.

            Во времена Евклида, вероятно, не было понятия о кривизне пространства, и даже сама Земля рассматривалась как абсолютно плоская поверхность.

Однако, Евклид, вероятно, не соглашался с таким определением. 

Заявление в те времена, что Земля это кривая поверхность, или тем более шар, не было бы правильно воспринято.

Вероятно, своим пятым постулатом Евклид отправил «зашифрованное сообщение» к будущему человечеству, показывая, что в его геометрии с плоскостью не все обстоит нормально, что она вымышлена - гипотетична, как его пятый постулат.

            Постулируя абсолютную плоскость, Евклид дал человечеству возможность создать удобные и простые для применения: геометрию, математику, физику и тем самым заложить фундамент для рывка в бесконечные просторы кривого пространства.

Признание факта, о невозможности существования абсолютной плоскости, вот, вероятно, краеугольный камень в основании создания новой геометрии, физики,  математики и путь познания вселенной.

Однако в науке до сих пор прямоугольный треугольник Пифагора, построенный на абсолютной плоскости  геометрии Евклида, является основой, во всемирно признанных теориях описания строения вселенной.

Возьмем преобразования Лоренца, в них значение √ 1- v²/c² получено из прямоугольника Пифагора.

Это противоречит букве и духу теории кривизны пространства, в котором нет места плоскому ПРЯМОУГОЛЬНОМУ треугольнику, абсолютно прямой линии и абсолютно плоской поверхности.

Снова вспомним Евклида и его определение точки.

«Точка есть то, что не имеет частей». В реальном мире  точка является геометрическим телом.

Но каким?

В постулатах Евклида ничего не говориться о толщине точки.

В реальном мире точку нельзя представить наименьшим кругом с отсутствующей толщиной.

Если мы добавим к определению точки еще и ее толщину, то она должна представлять собой наименьший шар.

            В таком случае мы уже не можем воспользоваться плоским треугольником Пифагора не имеющим толщину.

            На точке-шаре, как бы мы не уменьшали его размер, прямоугольный треугольник будет иметь три прямых угла и этот треугольник никак не сможет стать плоским. 

Пренебрежение значением второго порядка малости при замене треугольника на криволинейной поверхности прямоугольным, плоским треугольником, в микромире ведет к огромной ошибке.

Проводя расчеты для поверхностей, траекторий движения, у которых радиус кривизны стремиться к нулю, получаем, что при стремлении к нулю площади треугольника Евклида и Лобачевского, величина значения, второго порядка малости, то есть разница площадей или длин в этих геометриях, приобретает значение, чуть ли не равное самой площади треугольников или расстояний между точками.

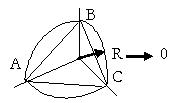
Рис.1

Легко представить эту разницу, достаточно построить упрощенную модель (рис.1) двухмерного треугольника Евклида в трехмерном треугольнике Лобачевского.

Площадь треугольника Лобачевского S_АВС = 4πR² /8 = πR² /2

Площадь треугольника Евклида, рассчитанная на основе прямоугольника Пифагора SАВС = R² √3/2

Как бы R не стремился к нулю, разница площадей плоского треугольника и треугольника на шаре будет отлична приблизительно на:

π/√3  раз.

Пренебрегать этой разницей или считать эту неточность величиной второго порядка малости, которую можно не брать в расчет, явно не корректно.

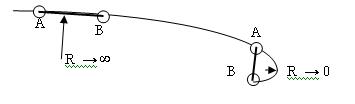
Рис.2

   Тоже происходит и с траекторией движения точки А из бесконечности в нуль - точку В, когда радиус кривизны стремиться к нулю (рис.2).

На участке, где R  → ∞ (рис.2 слева) катет  АВ, если применить прямоугольный треугольник Пифагора практически равен гипотенузе и мы попадаем в физику Ньютона

На участке АВ, где  R  → 0 (рис.2 справа), катет  АВ превращается в хорду  L, длина которой вычисляется по формуле:

L² = a(2R – a).

Вывод данной формулы приведен еще в III веке в  китайской книге «Математика в девяти книгах» и в задаче индийского математика VII века Брамагупты.

       Описание траектории электрона и его спина на основе реальных трехмерных кривых и объемных треугольников, а не на основе ломанных двумерных прямых и плоских прямоугольников позволит математикам попасть внутрь атома и раскрыть тайны неуловимого пространства.

Признавая неоценимый вклад физиков, работавших до третьего тысячелетия, следует признать, что они не смогли расшифровать тайну послания Евклида, заложенную им в пятый постулат.

Модели материи и пространства, созданные на основе прямоугольного прямоугольника Пифагора, следует признать двухмерными.

Третье тысячелетие должно стать тысячелетием создания основы, описывающей реальные трехмерные модели криволинейной материи и пространства.

Пятый постулат Евклида в 3D пространстве.

Представим  пятый постулат Евклида в общем виде в трехмерном пространстве.

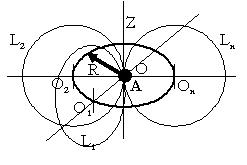
Рис.3

Через точку А (рис.3), заданной плоскости О₁, имеющей радиус кривизны стремящийся к бесконечности, с центром О₁, проведем прямую L₁, с радиусом кривизны стремящимся к бесконечности, и совпадающий с центром кривизны плоскости О₁. 

Переместим центр кривизны в точку О₂, и проведем через точку A прямую L₂, принадлежащую плоскости О₂, с центром кривизны плоскости О₂.

Как видим прямые L₁, L₂, не пересекаются, хотя имеют общую точку А.

Таким образом можно провести бесчисленное множество параллельных прямых L₁, L₂, …, L _{n →∞}   не принадлежащих данной плоскости, но имеющих общую точку А, при условии, что координаты центра кривизны каждой плоскости О₁, О₂, …, О_{n →∞},  описывают окружность О радиусом кривизны R →∞ вокруг оси Z.

Ось Z является общей касательной для всех рассматриваемых плоскостей.

В данном случае мы получаем пространственную фигуру тора, при равенстве R. В общем случае R может иметь отличные значения.

В реальном, физическом пространстве, радиус кривизны не бесконечен, а ограничен силами, определяемыми физическими свойствами среды и взаимодействием рассматриваемой области среды с другими областями. Эти свойства вызывают деформацию радиуса кривизны плоскости как по любой, так и по всем ее осям симметрии.

Из пятого постулата следуют условия:

1.             Координаты Z плоскости, а значит и прямой и задаваемой точки, как принадлежащих плоскости, равны. 

2.             Одна из координат X или Y задаваемой точки, не  принадлежит прямой.

3.             Прямая имеет только одну степень свободы.

4.        Центр кривизны прямой, параллельной заданной, для соблюдения параллельности может перемещаться только по одной оси.

Отсюда, пятый постулат Евклида, есть частный случай, описывающий, единственный вариант из  бесчисленного множества.

На плоскости, с заданным радиусом кривизны, через точку, находящуюся вне прямой, можно провести только одну прямую, параллельную данной, у которой хотя бы одна из координат центра кривизны  не совпадала с координатой центра кривизны  исходной.

 Рис.4

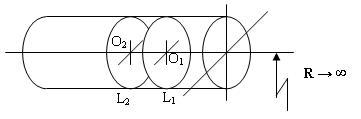
Такое толкование пятого постулата в общем виде описывает пространственную трубу (рис.4) с радиусом кривизны R →∞.

Введение понятия кривизны в описание плоскости и прямых, ведет к парадоксальному выводу:

Любая прямая при ее бесконечном продолжении является замкнутой кривой.

Действительно, если у прямой есть радиус кривизны, значит, есть и окружность, которую она формирует, вне зависимости какого радиуса, вплоть до бесконечного.

Отсюда у кривой прямой нет начала и нет конца.

Кривая, возникая из бесконечности проделав свой путь и, крутанувшись по бесконечному пространству, снова уходит в бесконечность.

Как можно отличить одну прямую от другой?

Если брать координаты начала и конца прямой, то они находятся в неопределенной бесконечности.

А если сравнивать радиусы кривизны «прямых»?

В этом случае мы сразу сможем отличить одну прямую от другой.

В реальном физическом мире все конечно. Значит и радиусы кривизны «прямых» и «плоскостей» конечны.

Означает ли это о конечности нашей вселенной?

Ведь согласно построенной модели кривой геометрии получается, что если преодолеть плоскость с радиусом кривизны, стремящимся к бесконечности можно попасть в потусторонний мир. Однако на этом пути нас встретит НЕПРЕОДОЛИМАЯ АБСОЛЮТНО ПРЯМАЯ КАСАТЕЛЬНАЯ к кривой.

А абсолютно прямая линия в реальной природе не существует (см. ниже).

Возможна ли геометрия потустороннего мира.

Для примера рассмотрим движение ракеты во время разгона.

 

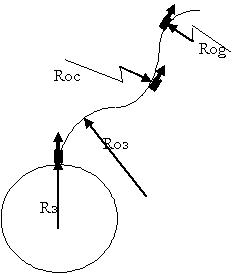
Рис.5

 

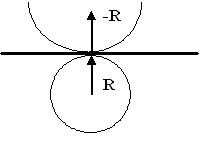
Рис.6